[科普中国]-球环

球环是一种特殊的球台，是平面上一小于半圆的弓形绕不穿过它的直径旋转一周所生成的几何体。也可以将球环看成是从球台内截去一个与球台共底的圆台或圆柱而成的几何体1。

球环的概念将一弓形绕不穿过它的一条直径旋转，所产生的立体称为球****环。弓形是指由一段圆弧与它所对弦所围成的图形。当弧是劣弧时，称为劣弓形，否则称为优弓形。如图1中的球环就是球台去掉中间的圆柱，图2中的球环就是球台去掉中间的圆台1。

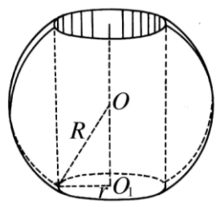
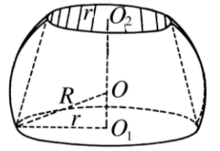
相关定理球环的体积 弓形绕不穿过它的直径旋转时，所产生的体积(球环的体积)是一个柱的体积的六分之一，这个柱的底是以弓形的弦为半径的圆，高则为这弦在轴上的射影2。

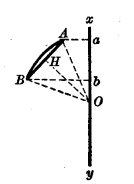
证明 设一圆O(图3)的弧AB及其弦所园的弓形绕通过O的轴xy旋旋，仍设ab为AB在xy上的射影。

当图形绕xy旋转时，圆扇形OAB产生的体积等于

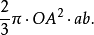另一方面，三角形OAB旋转时产生的体积等于面积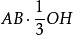(以OH表示圆心到弦AB的距离)，即等于

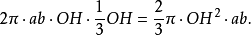
上面两个体积的差显然由球环的体积构成，因此它等于

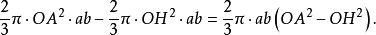
但在三角形OAH中有

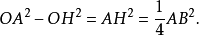
所以

球环AB的体积=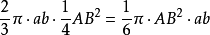，证毕2。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所