[科普中国]-楔体

楔体(Wedge)是一种特殊的拟柱体，是下底面是梯形或平行四边形，上底面是与下底面的平行边平行的线段的拟柱体。

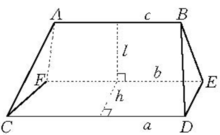
基本介绍楔体是一种特殊的拟柱体，将一个三棱柱(直三棱柱或斜三棱柱)用一个与三棱相交的截面(直截面或斜截面)去截开，所得的几何体称为楔体。它是一种拟柱体，下底面为梯形或平行四边形，上底面是与下底面的平行边平行的线段。图1中画出了楔体AB-CDEF。中国古算书《九章算术》中给出了当AE面垂直于CE面时被称为羡除的体积计算公式为1

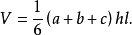
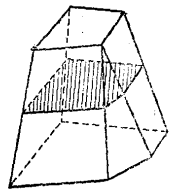
楔体与拟柱体拟柱体 所有顶点都在两个平行的平面上的多面体叫做拟柱体。它在这两个平面内的面叫做拟柱体的底面，其余各面叫做拟柱体的侧面，两底面之间的距离叫做拟柱体的高，通过高的中点且平行于底面的截面叫做拟柱体的中截面(图2)2。

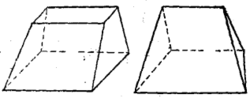
楔体 拟柱体的两底都是矩形，并且对应边平行，这种拟柱体叫做长方台（图3左）。如果拟柱体的下底面是梯形或平行四边形，上底面变成了与下底面平行的线段，这样的拟柱体叫做楔体（图3右）。

拟柱体除有长方台和楔体两种特殊情形外，从定义可知，还有下面一些特殊情形：

1.如果拟柱体的两底面是全等的多边形，并且对应边平行，则这样的拟柱体就是棱柱。

2.如果拟柱体的一个底面变为一点，则拟柱体就变为棱锥。

3.如果拟柱体的两底面是相似多边形，并且对应边平行，则这样的拟柱体就是棱台。

显然，正四棱台也是长方台的特殊情形，三棱柱也可以看作是楔体的特殊情形2。

拟柱体及楔体的体积公式

现在我们研究拟柱体体积公式一辛普松定理：

定理 任意拟柱体的体积，等于它的高h与上底面积S1，下底面积S2，中截面积S0四倍的和的六分之一。即：

V拟柱体=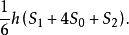

【例1】已知楔体下底上平行棱MN、CD的长是a、b，平行于它们的棱KL长为c，垂直于这些棱的直截面面积为S'，求楔体的体积。

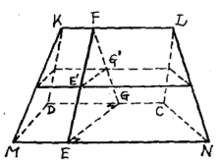
解 设楔体的直截面EFG与中截面的交线为E'G'(图4)因为楔体是拟柱体的特殊情形。

所以它的体积 V楔体=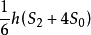

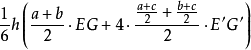因为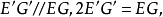

所以V楔体=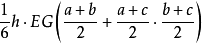

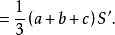
本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所