[科普中国]-塞尔伯格筛法

塞尔伯格筛法(Selberg sieve)是塞尔伯格(Selberg,Atle,1917.6.14-)提出的在数论中有广泛应用的一个初等方法，筛法的基本问题是估计筛函数S(A;P，z)的上界和正的下界。

基本介绍塞尔伯格筛法是在数论中有广泛应用的一个初等方法。设A是由有限个整数组成的集合(元素可以重复)，P是由无限个素数组成的集合(元素不能重复)，以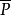 表示所有不属于P的素数组成的集合，再设z≥2是任意实数，并令

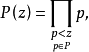函数

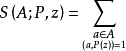称为筛函数，它表示集合A中没有小于z且属于P的素因子的元素的个数，亦即表示从集合A中筛去所有小于z且属于P的素因子的元素后所剩下的元素的个数.筛函数有下述性质1：

1.S(A;P，2)=|A| (|A|表示A中元素个数)；

2.S(A;P，z)≥0；

3.S(A;P，z1)≥S(A;P，z2)，2≤z1≤z2；

4.对任意的2≤ω≤z，有

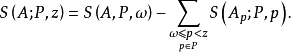其更重要的性质是：

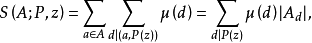其中μ(d)为默比乌斯函数，Ad表示A中所有能被d所整除的元素所组成的子集，并且筛函数S(A;P，z)的估计与集合Ad，d|P(z)有密切的关系。对于集合A及P，适当选取正数X>1及一个非负可乘函数ω(d)，μ(d)≠0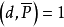， ，并设

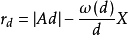及ω(d)满足条件：0