[科普中国]-维格纳3-j符号

维格纳 3-j 符号也称3-j符号，与量子力学中的克莱布希－高登系数有密切关系。

简介维格纳 3-j 符号也称3-j符号，与量子力学中的克莱布希－高登系数有密切关系。

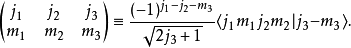
反演关系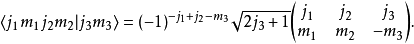

对称性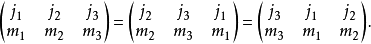

位相

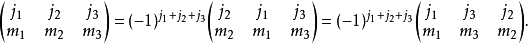
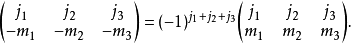
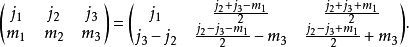
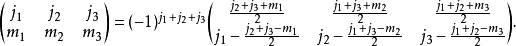
里奇对称性包括72类对称性 symmetries.

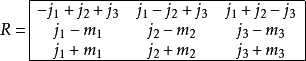
克莱布希－高登系数在量子力学中，克莱布希－高登系数（Clebsch–Gordan coefficients，简称CG 系数，又称向量耦合系数等）是两个角动量耦合时，它们的本征函数的组合系数。

从数学的角度，克莱布希－高登系数出现在紧李群的表示论中，它研究的是两个不可约表示的张量积如何分解成不可约表示的直和。

克莱布希－高登系数因阿尔弗雷德·克莱布什和保罗·哥尔丹而得名。2

角动量角动量在物理学中是与物体到原点的位移和动量相关的物理量。在经典力学中可被定义为物体到原点的位移（矢径）和其动量的叉积：

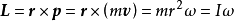
其中，表示以质点到旋转中心（轴心）的距离（标量值可以理解为半径的大小），方向由原点指向物体位置的矢量(即矢径)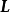，表示角动量，表示线速度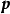，表示动量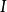，表示转动惯量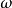，表示角速度(矢量)。角动量是矢量，且是轴矢量。其量纲为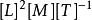，SI单位制中单位为。

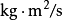角动量的方向：角动量是两个矢量的叉乘，在右手坐标系里遵循右手螺旋法则，即右手四指指向矢径的方向，转过一个小于180度的平面角后四指指向动量的方向，则大拇指所指的方向为角动量的方向。1

参见角动量算符及其一般理论

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所