分数化小数(change of fraction into decimal)是一种恒等变形,指将分数通过一定的法则化为小数的运算。因为每一个假分数,都可以化为整数或一个整数与一个真分数的和,而每个真分数又可以通过约分化为最简分数,所以,研究分数化小数,只需研究最简分数化小数1。
基本介绍分数化小数指将分数通过一定的法则化为小数的运算。
分数化小数可分为三种情况:
1.分数化为有限小数。一个最简分数能化为有限小数的充分必要条件是分母的质因数只有2和5。
2.分数化为纯循环小数。一个最简分数能化为纯循环小数的充分必要条件是分母的质因数里没有2和5,其循环节的位数等于能被该最简分数的分母整除的最小的99…9形式的数中9的个数。
3.分数化为混循环小数。一个最简分数能化为混循环小数的充分必要条件是分母既含有质因数2或5,又含有2和5以外的质因数。化成的混循环小数中,不循环的位数等于分母里的因素2或5的指数中较大的一个;循环节的位数,等于能被分母中异于2,5的因子整除的最小的99…9形式的数中,数9的个数1。
其他介绍除了以上所说的三种情况,分数化小数的方法还可区分成两种情况来说明2:
1.化分母是整十、整百....的分数为小数的方法。
(1)去分母移分子法。是指去掉分数的分母,把分子的小数点向左移动几位的方法。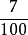 例如,把
例如,把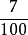 化成小数时,先去掉分母100,然后把分子7的小数点向左移动两位得0. 07,所以=0.07。
化成小数时,先去掉分母100,然后把分子7的小数点向左移动两位得0. 07,所以=0.07。
(2)关系法。是指根据分数与小数的关系来化的一种方法例如,化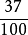 为小数时,根据“两位小数表示百分之几”的关
为小数时,根据“两位小数表示百分之几”的关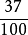 ,系可知改写后的小数为两位小数,所以=0.37。
,系可知改写后的小数为两位小数,所以=0.37。
分数改写成小数时,小数部分的数位不够,要用零补足,如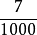 化成小数应是0. 007。
化成小数应是0. 007。
(3)读写法。是指根据小数的读法来改写的方法,例如将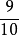 改写成小数时,可根据
改写成小数时,可根据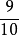 读作十分之九来写出小数0.9。
读作十分之九来写出小数0.9。
又例如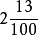 可根据读作二又百分之一十三,直接写出小数2.13。
可根据读作二又百分之一十三,直接写出小数2.13。
2.化分母不是整十、整百....的分数为小数的方法。
(1)相除法。是指用分子除以分母的一种化法。
例如,把 和
和 化成小数时,其相除过程如下:
化成小数时,其相除过程如下:

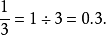
(2)性质法。是指利用分数的基本性质把分母化成是整十、整百,...的分数,然后再化成小数的方法。
例如,化 和
和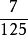 为小数时,过程分别如下2:
为小数时,过程分别如下2:
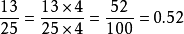
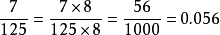
本词条内容贡献者为:
杜强 - 高级工程师 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国