[科普中国]-柯西一布尼亚科夫斯基不等式

柯西-布尼亚科夫斯基不等式(Cauchy-Bunjakovski inequality)是一种特殊不等式，指两个向量的长度积与其内积绝对值(模)的关系，欧氏空间或酉空间V中任意两个向量α与β必满足|(α，β)|≤|α|·|β|，等号成立的充分必要条件是：α与β线性相关，此不等式称为柯西-布尼亚科夫斯基不等式1。

基本介绍柯西-布尼亚科夫斯基不等式指两个向量的长度积与其内积绝对值(模)的关系，欧氏空间或酉空间V中任意两个向量α与β必满足|(α，β)|≤|α|·|β|，等号成立的充分必要条件是：α与β线性相关，此不等式称为柯西-布尼亚科夫斯基不等式。例如，在n维欧氏空间R中，上述不等式为

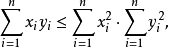又称为柯西不等式，由此可规定n维欧氏空间中两个向量的夹角

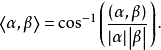
1821年，对于欧氏空间Rn，柯西(A.L.Cauchy) 证明了在一般情况的这一不等式；1859年，布尼亚科夫斯基(В.Я.Буняковский)证明并系统地应用了这一不等式；1885年，施瓦兹(H.A.Schwarz)在其文章《纪念文集》中论证了这个不等式，因而也称这个不等式为施瓦兹不等式1。

定理的证明设函数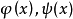和它们的平方在区间[a,b]上可积，证明柯西-布尼亚科夫斯基不等式2

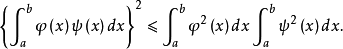
提示：考虑积分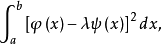其中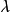为任意实数。

证明考虑积分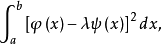，其中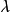为任意实数．从而有

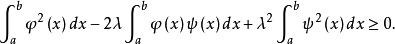这是关于变量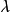的不等式，左端是二次三项式，于是，其判别式

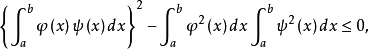即

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学