[科普中国]-迭代幂次

在数学里面，迭代幂次（亦作超-4运算），或可理解为迭代乘方、幂塔运算和超幂运算、广义幂指函数等等，是专指幂的下一个超运算级别，是幂运算的进一步拓展。

简介在数学里面，迭代幂次（亦作超-4运算），或可理解为迭代乘方、幂塔运算和超幂运算、广义幂指函数1等，是专指幂的下一个超运算级别。以下列举了首四个超运算级别，其中迭代幂次为第四级。2

定义对于任何正实数a及非负整数n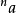， 被定义为：

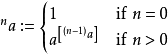
迭代乘方通常的解释是：

x+x+x=x*3，此3为表示3个相同的x相加；

x*x*x=x^3，此3表示相同的3个x相乘；

x^(x^x)=x^^3，此3表示连续3个x幂指运算且“^^”为新的运算。

可以继续推广。这就是迭代幂次的来由3。

从上述定义中可见，当计算被表达成幂塔的迭代幂次时，幂运算是先由最深层（以符号来表示，则最高级）的上标数做起。

例子如下：

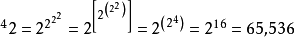
要注意，幂是不遵从结合律的，因此以其他顺序来计算上述表达式将会出现不一样的答案，例如：

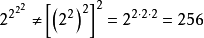
因此，幂塔一定要从上而下（或从右至左）来运算。在计算机程序中，此制式称为右结合律。

迭代幂次有多种表示方法，通常有：

标准符号记法： a[4]n 或者 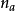；高纳德箭号表示法： a↑↑n；ASCII符号： a^^n；

其他如迭代指数法、阿克曼函数法、Hooshmand符号记法、超运算符号等不再赘述。

当a与n为互质时，我们可以透过欧拉定理来计算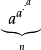 的最后m个小数位值。2

一般的，x^^0.5 是没有定义的（注意，它不等于x^0.5）。可以用一个假设解决此问题3。

相关条目

阿克曼函数

超运算

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学