[科普中国]-L理论

在数学中，代数L理论(L-theory)是K理论的二次型，而“L”的命名缘由即意味着它来自于“K理论”（L是K后面的一个字母）。L理论一个较为人所知的称呼是“厄米K理论”，它在割补理论(surgery theory)中占有重要地位。

简介在数学中，代数L理论(L-theory)是K理论的二次型，而“L”的命名缘由即意味着它来自于“K理论”（L是K后面的一个字母）。L理论一个较为人所知的称呼是“厄米K理论”，它在割补理论(surgery theory)中占有重要地位。1

K-理论在数学中，K-理论（K-theory）是多个领域使用的一个工具。在代数拓扑中，它是一种异常上同调，称为拓扑K-理论；在代数与代数几何中，称之为代数K-理论；在算子代数中也有诸多应用。它导致了一类K-函子构造，K-函子包含了有用、却难以计算的信息。

在物理学中，K-理论特别是扭曲K-理论出现在第二型弦理论，其中猜测它们可分类D-膜、拉蒙-拉蒙场以及广义复流形上某些旋量。具体细节参见K-理论 (物理)。1

二次型在数学中，二次型是一些变量上的二次齐次多项式。例如

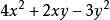是关于变量x和y的二次型。

二次型在许多数学分支，包括数论、线性代数、群论(正交群)、微分几何(黎曼测度)、微分拓扑(intersection forms of four-manifolds)和李代数(基灵型)中，占有核心地位。1

参见K理论

割补理论

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学