在数学分析中,半连续性是实值函数的一种性质,分成上半连续与下半连续,半连续性较连续性弱。
形式定义
设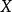 为拓扑空间,
为拓扑空间,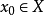 而
而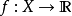 为实值函数。若对每个 ε > 0 都存在
为实值函数。若对每个 ε > 0 都存在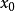 的开邻域
的开邻域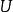 使得1
使得1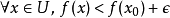 ,则称
,则称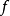 在
在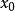 上半连续。该条件也可以用上极限等价地表述:
上半连续。该条件也可以用上极限等价地表述:
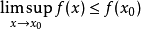 若
若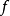 在
在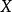 上的每一点都是上半连续,则称之为上半连续函数。
上的每一点都是上半连续,则称之为上半连续函数。
下半连续性可以准此定义:若对每个 ε > 0 都存在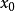 的开邻域
的开邻域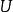 使得
使得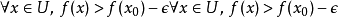 ,则称
,则称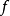 在
在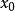 下半连续。用下极限等价地表述为:
下半连续。用下极限等价地表述为:
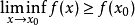 若
若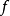 在
在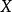 上的每一点都是下半连续,则称之为下半连续函数。
上的每一点都是下半连续,则称之为下半连续函数。
拓扑基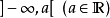 赋予实数线
赋予实数线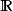 较粗的拓扑,上半连续函数可以诠释为此拓扑下的连续函数。若取基为
较粗的拓扑,上半连续函数可以诠释为此拓扑下的连续函数。若取基为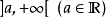 ,则得到下半连续函数。2
,则得到下半连续函数。2
例子
考虑函数
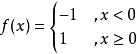 此函数在
此函数在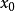 上半连续,而非下半连续。
上半连续,而非下半连续。
下整数函数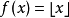 处处皆上半连续。同理,上整数函数
处处皆上半连续。同理,上整数函数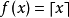 处处皆下半连续。
处处皆下半连续。
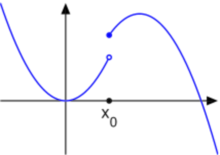
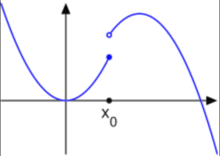
性质
一个函数在一点连续的充要条件是它在该点既上半连续也下半连续。
若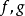 在某一 点上半连续,则
在某一 点上半连续,则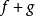 亦然;若两者皆非负,则
亦然;若两者皆非负,则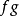 在该点也是上半连续。若
在该点也是上半连续。若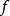 在一点上半连续,则
在一点上半连续,则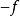 在该点下半连续,反之亦然。
在该点下半连续,反之亦然。
若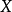 为紧集(例如闭区间),则其上的上半连续函数必取到极大值,而下半连续函数必取到极小值。
为紧集(例如闭区间),则其上的上半连续函数必取到极大值,而下半连续函数必取到极小值。
设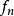 为下半连续函数序列,而且对所有
为下半连续函数序列,而且对所有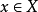 有
有
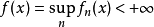
则 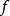 是下半连续函数。
是下半连续函数。
开集的指示函数为下半连续函数,闭集的指示函数为上半连续函数。3
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国