[科普中国]-可表函子

可表函子是在数学中范畴论里的概念，指从任意范畴到集合范畴的一种特殊函子。

这种函子将抽象的范畴表达成人们熟知的结构（即集合与函数），从而使得对集合范畴的了解可以尽可能应用到其它环境中。

定义设C 为局部小范畴，并记集合范畴为Set 。对 C 中的每个对象 A以Hom (A,-)指代将对象X 映到集合Hom (A,X) 的Hom函子。

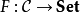函子是可表的当存在某个C中的对象A使得 F自然同构于Hom (A,X)。而满足

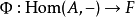
为自然同构的对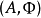 则称为 F的一个表示1。

从C到Set 的反变函子G不过是（协变）函子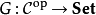，常被称作预层。与协变的情况相似，预层是可表的当它自然同构与某个反变的Hom函子 Hom (-,A)，其中 A是C 中的某个对象。

泛元素根据米田引理，从Hom (-,A)到 F 的自然变换与集合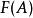一一对应。给定自然变换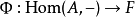，与之对应的元素 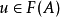由

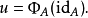
给出。反之，给定元素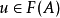，可以如下定义自然变换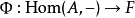

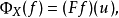
其中 f 是Hom (A,X)中的任意元素。为了得到 F 的表示，我们需要确定 u诱导的自然变换何时会是同构。这引导出如下定义：

函子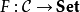的泛元素是由C中的对象 A与 F(A) 中的元素 u 组成的一对 (A,u)，使得对于任意满足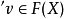的对 (X,v)，都存在唯一映射 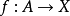使得。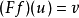

泛元素还可看作从单点集合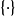到函子{ F}的泛态射，又或者看作{ F}的元素范畴中的始对象。

性质唯一性函子的表示在同构的意义下唯一。

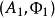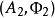换言之，如果与 表示同一个函子，那么存在唯一的同构 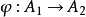使得

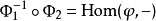
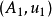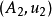用泛元素的语言表述如下：如果与 表示同一个函子，那么存在唯一的同构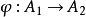使得

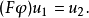
保极限性可表函子自然同构于Hom函子，因而享有许多后者的性质。尤其值得注意的是，（协变）可表函子保持所有极限。由此可得，未能保持某些极限的函子都不是可表的。

相似地，反变可表函子把余极限映到极限。

左伴随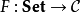如果函子 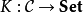带有左伴随，那么它就可由 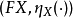表示；这里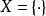是某个单元素集合，而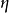是伴随的单位。

反之，如果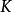由对(A,u)表示，且 A 的任意上幂在 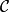中都存在，那么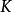拥有左伴随F，后者将任意集合 I映到 A 的I 次上幂。

所以，如果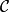是带所有上幂的范畴，则函子 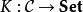是可表的当且仅当它拥有左伴随。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学