平均数不等式,或称平均值不等式、均值不等式,是数学上的一组不等式,也是基本不等式的推广。
定义
平均数不等式,或称平均值不等式、均值不等式,是数学上的一组不等式,也是基本不等式的推广。它是说:
如果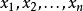 是正数,则
是正数,则
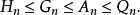
其中:
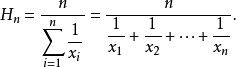
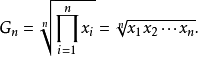
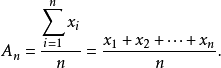
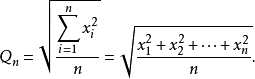
当且仅当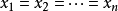 ,等号成立。即对这些正数:调和平均数≤几何平均数≤算术平均数≤平方平均数(方均根)简记为:“调几算方”。
,等号成立。即对这些正数:调和平均数≤几何平均数≤算术平均数≤平方平均数(方均根)简记为:“调几算方”。
证明方法
关于均值不等式的证明方法有很多,数学归纳法(第一数学归纳法或反向归纳法)、拉格朗日乘数法、琴生不等式法、排序不等式法、柯西不等式法等等,都可以证明均值不等式,在这里简要介绍数学归纳法证明n维形式的均值不等式的方法:1
用数学归纳法证明,需要一个辅助结论。
引理:设A≥0,B≥0,则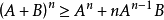 ,且仅当B=0时取等号。
,且仅当B=0时取等号。
引理的正确性较明显,条件A≥0,B≥0可以弱化为A≥0,A+B≥0,可以用数学归纳法证明。
原题等价于: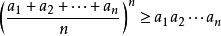 , 当且仅当
, 当且仅当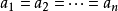 时取等号。
时取等号。
当n=2时易证;
假设当n=k时命题成立,即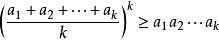 , 当且仅当
, 当且仅当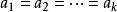 时取等号。
时取等号。
那么当n=k+1时,不妨设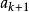 是
是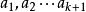 中最大者,则
中最大者,则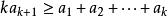 。
。
设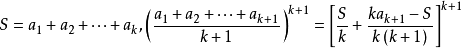 ,根据引理
,根据引理
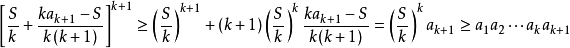 ,当且仅当
,当且仅当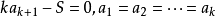 时,即
时,即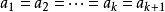 时取等号。
时取等号。
利用琴生不等式法也可以很简单地证明均值不等式,同时还有柯西归纳法等方法。
参见
算术-几何平均值不等式
幂平均不等式
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国