[科普中国]-递推列

递推列(recursive sequence)亦称递归列，指由前面的项能推出后面的项的数列，线性递推列是特殊的递推列。例如等差数列与等比数列就是递推列，也是线性递推列1。

基本介绍递推列指由前面的项能推出后面的项的数列，对所有n>p，满足形如an=f(an-1，an-2，…，an-p)的关系式的序列{an}，其中f为某个函数。p是某个固定的正整数，a1，a2，…，ap为已知数，p称为这个递推列的阶数，上述关系式称为递推公式，给定a1，a2，…，ap，可以从它得到所有an。

形如an+c1an-1+c2an-2+…+cpan-p=0(c1，c2，…，cp是常数)的递推公式称为线性递推公式，相应的序列称为线性递推列，最简单的递推列是一阶递推列，即满足an=f(an-1)的序列{an}，它又称迭代列。等差数列与等比数列都是线性的迭代列1。

根据以上定义，将F和V均取为Q，则我们熟悉的Fibonacci序列是线性递推列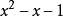，构成它的一个特征多项式。我们知道，对于一个线性递推列，在已知其特征多项式及最初的几个取值时，可以通过递推的方法快速计算其后继序列，下面我们举一些线性代数中涉及的线性递推列的例子，它们在后而的算法中扮演了重要角色2。

相关介绍【例1】本例给出线性代数中一些熏要的线性递推列，这里最关键的是利用了线性代数中的Caley-Hamilton定理[，以下F均表示一般域。

1．取V=Fn×n，A∈V为任意方阵，则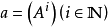为线性递推列，A的极小多项式与特征多项式都是a的特征多项式。

2．设V=Fn，A∈Fn×n，b∈Fn为任意向量，注意到(Ai)的任意特征多项式也将(Aib)化为零，故(Ajb)也为线性递推列。由a的元素生成的V中的线性子空间称为A与b的Krylov子空间。

3．设V=Fn，A∈Fn×n，b，u∈Fn为V中的任意向量，则(Aib)的任意特征多项式同样将(uTAib)化为零，故(uTAi)b也为线性递推列2。

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学