[科普中国]-布尔乘法

布尔乘法亦称布尔交(记为∩)或布尔合取(记为∧)或布尔积，指布尔代数B=〈B，+，·，′，0，1〉中记为·的二元运算，对任意给定的两个元素a，b∈B，经乘法运算后得到一个确定的元素d∈B，记为d=a·b，d称为a，b的布尔积1。

基本介绍两个变量的布尔乘法(Boolean multidplication，即ANDing)记为AB，并把它称为乘积项。三个变量的布尔乘法可以表示为ABC，类似地，可以表示任意多个变量。当然，也可以用其他字母来代替A，B，C。这与常规代数的变量乘法的表示相同。有时在代数表达式中，变量之间会使用圆点(·)来表示乘法，如A**·**B；有时还会使用圆括号，如(A)(B)，特别是当表达式中项数很多时1。

在元素不多的情形下，常可用列表法确定布尔乘法，下面是含且仅含4个元素的布尔代数的乘法表，表中最左一列表示乘法的第一个元素，最上一行表示乘法的第二个元素，各对应行列交叉处记的是两者的布尔积。特别，对二元布尔代数，其布尔乘法当且仅当两个元素a，b∈B都是1时，a·b才是1，否则a·b是0(参见“二元布尔代数”)1。

布尔乘法的运算律下面的运算律也称为布尔代数的运算律。

布尔代数的运算律是布尔代数的基本运算法则，布尔代数〈B，+，·，′，0，1〉有如下运算律，对B中任意元素a，b，c，有1：

1.结合律：(a+b)+c=a+(b+c) ，

(a·b)·c=a·(b·c).

2.交换律：a+b=b+a， a·b=b·a.

3.分配律：a·(b+c)=(a·b)+(a·c)，

a+(b·c)=(a+b)·(a+c).

4.吸收律：a+a·b=a， a·(a+b)=a.

5.幂等律：a+a=a， a·a=a.

6.德·摩根律(反演律)：(a+b)′=a′·b′，

(a·b)′=a′+b′.

7.对合律(双重否定律)：(a′)′=a.

8.互补律：a+a′=1， a·a′=0.

9.零一律(幺元律)：a+0=a， a·1=a.

10.囿元律(极元律)：a+1=1， a·0=0.

布尔乘法和与门电路根据布尔代数，与门是一个乘法器。这与常规的十进制乘法运算相同，因为0乘以1等于0，1乘以1等于1，正如与门真值所示。布尔乘法等价于一个与门电路，其基本法则用与门表示如下2：

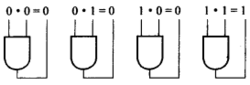
与门的布尔表达式

（1）2输人与门运算的布尔代数表达式为：

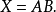该布尔表达式表明：输出X等于输入A和B的乘积(与)，读作“X等于A与B”。

为了计算X=AB，先看看该式是如何描述与门运算的，将1或0代人每个变量。两个变量，共有22=4种输入状态组合。

当A=0，B=0：X=AB=0·0=0

当A=0，B=1：X=AB=0·1=0

当A=1，B=0：X=AB=1·0=0

当A=1，B=1：X=AB=1·1=1

（2）3输人与门运算的布尔代数表达式为：

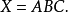
遍历所有可能的输入状态组合(23=8)，代人二进制数值，计算其输出结果。对应的真值表参见表12。

|| || 表1

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学