有限布尔代数(finite Boolean algebra)是一种常用的布尔代数,指论域B是有限集的布尔代数。有限布尔代数的论域B的元素个数必是2的方幂2n(n=1,1,2,…),n=0时的布尔代数是仅含一个元素的退化布尔代数,n=1时的布尔代数仅含0和1两个元素,称为二元布尔代数,区分有限与无限布尔代数是有意义的,因为有限布尔代数必是原子布尔代数,从而它同构于某个集A的所有子集构成的布尔代数;但一个无限布尔代数未必是一个原子布尔代数,故它无上述性质1。
基本介绍定义1 具有有限个元素的布尔代数称为有限布尔代数。
对于有限布尔代数,有以下的结论:对于每一正整数n,必存在含有2n个元素的布尔代数;反之,任一有限布尔代数,它的元素个数必为2的幂次。元素个数相同的布尔代数都是同构的。
定义2 设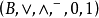 是一个布尔代数,a∈B且a≠0,若任意x∈B,有x∧a=a或x∧a=0, 则称元素a为原子。
是一个布尔代数,a∈B且a≠0,若任意x∈B,有x∧a=a或x∧a=0, 则称元素a为原子。
显然原子是0的覆盖,且若元素a覆盖0,则a必是原子2。
相关定理定理1 设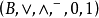 是一个布尔代数,a, b∈B是B的原子。若a≠b,则a∧b=02。
是一个布尔代数,a, b∈B是B的原子。若a≠b,则a∧b=02。
**证明:**假设a∧b≠0,由于a是原子,所以a∧b=b∧a=a。又b是原子,因此a∧b=b, 从而得到a=b,与已知条件a≠b矛盾。
定理2 设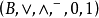 是一个有限布尓代数,任意b∈B,若b≠0,则至少存在一个原子a,使得a
是一个有限布尓代数,任意b∈B,若b≠0,则至少存在一个原子a,使得a




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国