生成随机网络(GSN)由两个条件概率分布参数化,是去噪自编码器的推广,除可见变量(通常表示为x )之外,在生成马尔可夫链中还包括潜变量h。它提出之初被用于对观察数据x的概率分布p(x)进行隐式建模。
基本概念生成随机网络(generative stochastic network, GSN)1是去噪自编码器的推广,除可见变量(通常表示为 )之外,在生成马尔可夫链中还包括潜变量
)之外,在生成马尔可夫链中还包括潜变量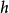 。
。
GSN 由两个条件概率分布参数化,指定马尔可夫链的一步:
(1)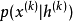 指示在给定当前潜在状态下如何产生下一个可见变量。这种 ‘‘重建分布’’ 也可以在去噪自编码器、 RBM、 DBN 和 DBM 中找到。
指示在给定当前潜在状态下如何产生下一个可见变量。这种 ‘‘重建分布’’ 也可以在去噪自编码器、 RBM、 DBN 和 DBM 中找到。
(2)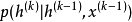 指示在给定先前的潜在状态和可见变量下如何更新潜在状态变量。
指示在给定先前的潜在状态和可见变量下如何更新潜在状态变量。
去噪自编码器和 GSN 不同于经典的概率模型(有向或无向),它们自己参数化生成过程而不是通过可见和潜变量的联合分布的数学形式。相反,后者如果存在则隐式地定义为生成马尔可夫链的稳态分布。存在稳态分布的条件是温和的,并且需要与标准 MCMC 方法相同的条件。这些条件是保证链混合的必要条件,但它们可能被某些过渡分布的选择(例如,如果它们是确定性的)所违反。2
训练准则我们可以想象 GSN 不同的训练准则。2
由 Bengio等1提出和评估的只对可见单元上对数概率的重建,如应用于去噪自编码器。通过将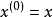 夹合到观察到的样本并且在一些后续时间步处使生成
夹合到观察到的样本并且在一些后续时间步处使生成 的概率最大化,即最大化
的概率最大化,即最大化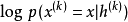 ,其中给定
,其中给定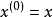 后,
后,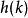 从链中采样。为了估计相对于模型其他部分的
从链中采样。为了估计相对于模型其他部分的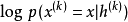 的梯度, Bengio等使用了重参数化技巧。
的梯度, Bengio等使用了重参数化技巧。
回退训练过程可以用来改善训练 GSN 的收敛性1。
重参数化技巧传统的神经网络对一些输入变量 x 施加确定性变换。当开发生成模型时,我们经常希望扩展神经网络以实现 x 的随机变换。这样做的一个直接方法是使用额外输入 z(从一些简单的概率分布采样得到,如均匀或高斯分布)来增强神经网络。神经网络在内部仍可以继续执行确定性计算,但是函数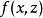 对于不能访问 z 的观察者来说将是随机的。假设
对于不能访问 z 的观察者来说将是随机的。假设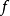 是连续可微的,我们可以使用反向传播计算训练所需的梯度。
是连续可微的,我们可以使用反向传播计算训练所需的梯度。
作为示例,让我们考虑从均值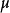 和方差
和方差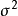 的高斯分布中采样 y 的操作:
的高斯分布中采样 y 的操作:
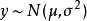 因为 y 的单个样本不是由函数产生的,而是由一个采样过程产生,它的输出会随我们的每次查询变化,所以取 y 相对于其分布的参数
因为 y 的单个样本不是由函数产生的,而是由一个采样过程产生,它的输出会随我们的每次查询变化,所以取 y 相对于其分布的参数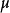 和
和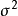 的导数似乎是违反直觉的。然而,我们可以将采样过程重写,对基本随机变量
的导数似乎是违反直觉的。然而,我们可以将采样过程重写,对基本随机变量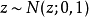 进行转换以从期望的分布获得样本:
进行转换以从期望的分布获得样本:
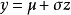 我们将其视为具有额外输入 z 的确定性操作,可以通过采样操作来反向传播。至关重要的是,额外输入是一个随机变量,其分布不是任何我们想对其计算导数的变量的函数。如果我们可以用相同的 z 值再次重复采样操作,结果会告诉我们
我们将其视为具有额外输入 z 的确定性操作,可以通过采样操作来反向传播。至关重要的是,额外输入是一个随机变量,其分布不是任何我们想对其计算导数的变量的函数。如果我们可以用相同的 z 值再次重复采样操作,结果会告诉我们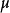 或
或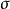 的微小变化将会如何改变输出。
的微小变化将会如何改变输出。
能够通过该采样操作反向传播允许我们将其并入更大的图中。我们可以在采样分布的输出之上构建图元素。例如,我们可以计算一些损失函数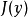 的导数。我们还可以构建这样的图元素,其输出是采样操作的输入或参数。例如,我们可以通过
的导数。我们还可以构建这样的图元素,其输出是采样操作的输入或参数。例如,我们可以通过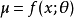 和
和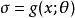 构建更大的图。在这个增强图中,我们可以通过这些函数的反向传播导出
构建更大的图。在这个增强图中,我们可以通过这些函数的反向传播导出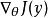 。
。
在该高斯采样示例中使用的原理能更广泛地应用。我们可以将任何形为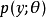 或
或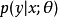 的概率分布表示为
的概率分布表示为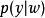 ,其中
,其中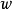 是同时包含参数
是同时包含参数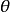 和输入
和输入 的变量 (如果适用的话)。给定从分布
的变量 (如果适用的话)。给定从分布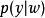 采样的值
采样的值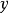 (其中
(其中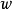 可以是其他变量的函数),我们可以将
可以是其他变量的函数),我们可以将
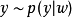 其中
其中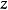 是随机性的来源。只要
是随机性的来源。只要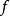 是几乎处处连续可微的,我们就可以使用传统工具(例如应用于
是几乎处处连续可微的,我们就可以使用传统工具(例如应用于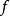 的反向传播算法)计算
的反向传播算法)计算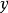 相对于
相对于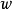 的导数。至关重要的是,
的导数。至关重要的是,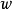 不能是
不能是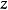 的函数,且
的函数,且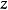 不能是
不能是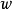 的函数。这种技术通常被称为 重参数化技巧(reparametrization trick)、 随机反向传播(stochastic back-propagation) 或扰动分析(perturbation analysis)。2
的函数。这种技术通常被称为 重参数化技巧(reparametrization trick)、 随机反向传播(stochastic back-propagation) 或扰动分析(perturbation analysis)。2
回退训练过程回退训练过程由 Bengio等3提出,作为一种加速去噪自编码器生成训练收敛的方法。不像执行一步编码-解码重建,该过程有代替的多个随机编码-解码步骤组成(如在生成马尔可夫链中),以训练样本初始化,并惩罚最后的概率重建(或沿途的所有重建)。
训练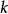 个步骤与训练一个步骤是等价的(在实现相同稳态分布的意义上),但是实际上可以更有效地去除来自数据的伪模式。2
个步骤与训练一个步骤是等价的(在实现相同稳态分布的意义上),但是实际上可以更有效地去除来自数据的伪模式。2
判别性GSNGSN的原始公式1用于无监督学习和对观察数据 的
的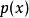 隐式建模,但是我们可以修改框架来优化
隐式建模,但是我们可以修改框架来优化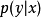 。
。
例如, Zhou and Troyanskaya4以如下方式推广 GSN,只反向传播输出变量上的重建对数概率,并保持输入变量固定。他们将这种方式成功应用于建模序列蛋白质二级结构),并在马尔可夫链的转换算子中引入(一维)卷积结构。重要的是要记住,对于马尔可夫链的每一步,我们需要为每个层生成新序列,并且该序列于在下一时间步计算其他层的值(例如下面一个和上面一个)的输入。
因此, 马尔可夫链确实不只是输出变量(与更高层的隐藏层相关联),并且输入列仅用于条件化该链,其中反向传播使得它能够学习输入序列如何条件化由马尔夫链隐含表示的输出分布。因此这是在结构化输出中使用 GSN 的一个例子。
Zöhrer and Pernkopf5引入了一个混合模型,通过简单地添加(使用不同的权重)监督和非监督成本即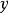 和
和 的重建对数概率,组合了监督目标(如上面的工作)和无监督目标(如原始的 GSN)。 Larochelle and Bengio6 以前RBM 中就提出了这样的混合标准。他们展示了在这种方案下分类性能的提升。 2
的重建对数概率,组合了监督目标(如上面的工作)和无监督目标(如原始的 GSN)。 Larochelle and Bengio6 以前RBM 中就提出了这样的混合标准。他们展示了在这种方案下分类性能的提升。 2
本词条内容贡献者为:
何星 - 副教授 - 上海交通大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国