[科普中国]-抛物柱面坐标系

抛物柱面坐标系（英语：Parabolic cylindrical coordinates）是一种三维正交坐标系。

简介抛物柱面坐标系（英语：Parabolic cylindrical coordinates）是一种三维正交坐标系。往 z-轴方向延伸二维的抛物线坐标系，则可得到抛物柱面坐标系。其坐标曲面是共焦的抛物柱面。抛物柱面坐标可以应用于许多物理问题。例如，物体边缘的位势论。1

基本定义直角坐标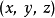 可以用抛物柱面坐标 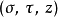表示为2

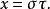
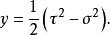
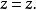其中， 。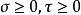

坐标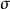 为常数的曲线形成共焦的，凹性往 +y-轴的抛物柱面：

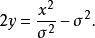而坐标 为常数的曲线形成共焦的，凹性往 -y-轴的抛物柱面：

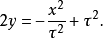这些抛物柱面的焦线的位置都在 z-轴。

径向距r的公式为

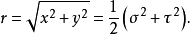当解析经典力学的反平方连心力问题时，假若采用抛物柱面坐标的哈密顿-亚可比方程式，则会用到这很有用的公式。参阅拉普拉斯-龙格-冷次向量。

标度因子抛物柱面坐标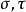 的标度因子相等；而 z的标度因子是 1 ：

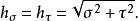
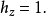
无穷小体积元素是

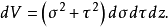
拉普拉斯算子是

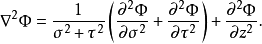
其它微分算子，像 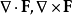，都可以用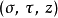坐标表示，只要将标度因子代入在正交坐标系条目内对应的一般公式。

应用抛物柱面坐标有一个经典的应用，这是在解析像拉普拉斯方程或亥姆霍兹方程这类的偏微分方程式。在这些方程式里，抛物柱面坐标允许分离变数法的使用。

本词条内容贡献者为:

杨明 - 副教授 - 西南大学