[科普中国]-勒贝格-斯蒂尔杰斯积分

勒贝格-斯蒂尔杰斯积分(英语：Lebesgue integral)是现代数学中的一个积分概念，它将积分运算扩展到任何测度空间中。在最简单的情况下，对一个非负值的函数的积分可以看作是函数图像与x轴之间的面积。勒贝格积分则将积分运算扩展到更广的函数（可测函数），并且也扩展了可以进行积分运算的集合（可测空间）。最早的积分运算对于非负值的函数来说，其积分相当于使用求极限的手段来计算一个多边形的面积（也就是黎曼积分），但这过程需要函数足够规则。但是随着对更加不规则的函数的积分运算的需要不断产生（比如为了讨论数学分析的极限过程中导致的函数，或者出于概率论的需求），很快就产生了对更加广义的求极限手段的要求来定义相应的积分运算。

引入在闭区间a和b之间对函数 f的积分可以被看作是 f的函数图像下的面积。对于多项式这样比较常见的函数来说这个定义简而易懂。但是对于更加稀奇古怪的函数来说它是什么意思呢？广义地来说，对于什么样的函数“函数图像下的面积”这个概念有意义？这个问题的答案具有很大的理论性和实际性意义。1

19世纪里在数学中有把整个数学理论放到一个更加坚固的基础上的趋势。在这个过程中数学家也试图给积分计算提供一个稳固的定义。波恩哈德·黎曼提出的黎曼积分成功地为积分运算提供了一个这样的基础。黎曼积分的出发点是构造一系列容易计算的面积，这些面积最后收敛于给定的函数的积分。这个定义很成功，为许多其它问题提供了有用的答案。

但是在求函数序列的极限的时候黎曼积分的效果不良，这使得这些极限过程难以分析。而这个分析比如在研究傅里叶级数、傅里叶变换和其它问题时却是极其重要的。勒贝格积分能够更好地描述在什么情况下积分有极限。勒贝格积分所构造出的容易计算的面积与黎曼积分所构造的不同，这是勒贝格积分更加成功的主要原因。勒贝格的定义也使得数学家能够计算更多种类的函数的积分。比如输入值为无理数时函数值为0，输入值为有理数时函数值为1的狄利克雷函数没有黎曼积分，但是有勒贝格积分。

推导以下的介绍是遵循最常见的勒贝格积分的介绍进行的。在这个介绍中积分理论分两部分：

可测集和在这些集合上可以进行的测量的理论

可测函数和对这些函数积分的理论

测度理论最初测度理论是用来对欧几里得空间中直线的长度，以及更广义地，欧几里得空间的子集的面积和体积进行仔细分析发展出来的。它尤其可以为 R的哪些子集拥有长度这个问题提供一个系统性的回答。后来发展的集合论证明，实际上不可能为 R的所有子集都分配一个长度，且保持天然的可加性和平移不变的性质。因此给出一个合适的，可测量的子集类是一个关键的前提。

当然，黎曼积分隐含了长度的概念。事实上计算黎曼积分的元素是[a,b]×[c,d]所组成的长方形，它的面积为(b−a)(d−c)。b−a是这个长方形的宽度，而d−c则是其高度。黎曼只能用平面的长方形来估算曲线下的面积，因为当时还没有其它适当的理论来测量更一般的集合。

在大多数现代的教科书中测度和积分都是公理性的。也就是说测度是一个定义在集合 E的某些子集组成的集合 X上的函数μ，这些子集必须拥有一定的特征。在许多不同的情况下这些特征成立。

积分从一个测度空间(E,X,μ)出发，E是一个集合，X是由 E的子集构成的σ代数，μ是定义在 X上的测度。

在勒贝格理论中只有对所谓的可测函数才能够进行积分。一个函数f被称为是可测的，假如每个区间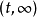 的的原像是 E中的可测集合，也就是：

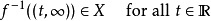
若

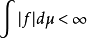
则 f被称为勒贝格可积的。在这种情况下，两个积分均满足

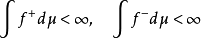
因此可以定义

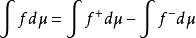事实上这个定义给出了具有良好特性的积分。

本词条内容贡献者为:

任毅如 - 副教授 - 湖南大学