[科普中国]-初等复变函数

初等复变函数是实变量初等函数在复数域中的推广。复变量的初等函数的定义形式上与初等函数相同，只不过它们的定义域已由实数集合推广到复数域中。

定义

初等复变函数是实变量初等函数在复数域中的推广。

初等函数

在实函数中，常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数这六类函数称为基本初等函数，而一切可由基本初等函数经过有限次四则运算和有限次复合生成的函数称为初等函数。

复变量的初等函数

复变量的初等函数的定义形式上与初等函数相同，只不过它们的定义域已由实数集合推广到复数域中。

性质

实变量的初等函数推广到复数域后，在实数域中保持它们原有的性质，但在复数域中具有一些新的性质，如复变指数函数的周期性、复变对数函数的无穷多值性、复变正弦函数与复变余弦函数的无界性等。

从这些新的性质可以看出，只有把这些函数从实数域推广到复数域，才能更全面、更深刻地揭示它们的本质。1

类型复变根式函数

(radical function of a complex variable)

复变根式函数是实变量根式函数在复数域中的推广。

形如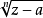，的函数称为复变根式函数，其中n是大于 1的正整数，a是复常数。

复变指数函数

(exponent function of a complex variable)

复变指数函数是实变量指数函数在复数域中的推广。

形如ez=ex+iy=ex(cos y+isin y)的函数称为复变指数函数。

复变一般指数函数

(general exponent function of a complex variable)

复变一般指数函数是实变量一般指数函数在复数域中的推广。

若a≠0，∞，则称函数w=az=ezlog a为复变一般指数函数。

复变幂函数

(power function of a complex variable)

复变幂函数是实变量幂函数在复数域中的推广。

形如w=za-ealogz(z≠0，∞，a为复常数)的函数称为复变幂函数。

复变对数函数

(logarithmic function of a tomplex variable)

复变对数函数是实变量对数函数在复数域中的推广。

若ew=z(z≠0，∞)，则复数w称为复数z的对数，记为w=Logz=log|z|+i(arg z+2kπ)(k=0,±1,±2,...}。若限定-π