辛格定理(theorem of Singer)是关于一类循环差集的存在性定理,该定理由辛格(J.Singer)于1938年利用有限射影几何证得1。
基本介绍若q为素数幂,则存在
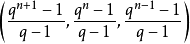 循环差集。
循环差集。
该定理由辛格(J.Singer)于1938年利用有限射影几何证得,将有限域GF(q)上的n+1维非零向量x=(x0,x1,…,xn)取作n维射影几何的点,当b为GF(q)中非零元时,把bx与x看做相同的点,这些点的集合记为PG(n,q),若ξ为扩域GF(qn+1)中的原根,则ξi与ξj表示PG(n,q)中相同点的充分必要条件为i≡j(mod v),这里
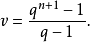
于是,PG(n,q)中的所有点可表为ξ0,ξ1,…,ξv-1.设y1,y2,…,yn是GF(q)上n个线性无关的n+1维向量,把一切向量b1y1+b2y2+…+bnyn(式中bi∈GF(q))所对应的点的集合称为一个超平面,其中的点可表为1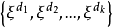 ,这里
,这里
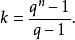
辛格证明:{d1,d2,…,dk}是循环群Zv中的(v,k,λ)差集,其中,λ=(qn-1-1)/(q-1)。
辛格定理的证明J.Singer于1938年引入了差集的概念并利用有限域上n维射影几何中的超平面构作了一类重要的循环差集2。
定理1(Singer)设q为素数幂,n≥2,又设
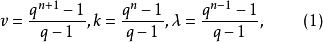 则存在Zv中(v,k,λ)-差集, 使得由此差集的全体平移组成的循环对称设计与以PG(n,q)中的点作元素,以超平面为区组所得到的SB(k,λ;v)同构。
则存在Zv中(v,k,λ)-差集, 使得由此差集的全体平移组成的循环对称设计与以PG(n,q)中的点作元素,以超平面为区组所得到的SB(k,λ;v)同构。
证 设V为Fq上n+1维向量空间,则V的1维子空间便是PG(n,q)中的点,V的n维子空间便是PG(n,q)中的超平面2。
设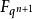 为Fq的n+1次扩域,α为
为Fq的n+1次扩域,α为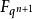 的一个本原元,
的一个本原元,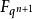 可看作Fq上的一个n+1维向量空间,它以1,α,...,αn为一组基,取此空间作为V。
可看作Fq上的一个n+1维向量空间,它以1,α,...,αn为一组基,取此空间作为V。
对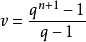 ,
,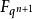 中的q-1个元素
中的q-1个元素
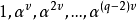 都是Fq上方程xq-1=1的根。由此它们就是Fq的全部非零元素,于是Fq中任一非零元t必可表成
都是Fq上方程xq-1=1的根。由此它们就是Fq的全部非零元素,于是Fq中任一非零元t必可表成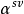 的形式,由此
的形式,由此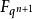 中两个非零元αi与αj代表V中同一个1维子空间的充分必要条件是存在Fq中的元素t=
中两个非零元αi与αj代表V中同一个1维子空间的充分必要条件是存在Fq中的元素t=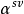 使
使
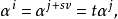 亦即
亦即
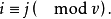 于是
于是
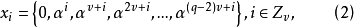 则
则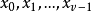 便是V中全部1维子空间亦即PG(n,q)中全部v个点,映射
便是V中全部1维子空间亦即PG(n,q)中全部v个点,映射
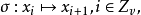 是PG(n,q)的一个自同构,σ生成一个v阶循环群G=
是PG(n,q)的一个自同构,σ生成一个v阶循环群G=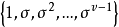 .G传递地作用在PG(n,q)中全体点的集合上,且G也传递地作用在全体超平面的集合上,由于
.G传递地作用在PG(n,q)中全体点的集合上,且G也传递地作用在全体超平面的集合上,由于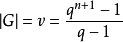 ,因此G在PG(n,q)中全体点的集合和全体超平面的集合上都是正则的.故若令D为由以全体超平面为区组,全体点为元素所组成的SB(k,λ;v)。则D是一个循环设计,令
,因此G在PG(n,q)中全体点的集合和全体超平面的集合上都是正则的.故若令D为由以全体超平面为区组,全体点为元素所组成的SB(k,λ;v)。则D是一个循环设计,令
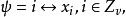 则
则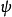 是Zv中元素与PG(n,q)中的点之间的一个1-1对应,设S为PG(n,q)的一个超平面,令
是Zv中元素与PG(n,q)中的点之间的一个1-1对应,设S为PG(n,q)的一个超平面,令
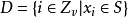 则D便是Zv中的一个(v,k,λ)-差集,由D的全体平移作区组所得的循环设计与D同构。
则D便是Zv中的一个(v,k,λ)-差集,由D的全体平移作区组所得的循环设计与D同构。
Singer定理所得到的差集叫Singer差集2。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国