[科普中国]-无解性

无解性，也叫做无可行解性，是指在线性规划问题中，使得可行域为空集的性质。

基本内容原问题，又称原线性规划问题，是指每一个线性规划的原始问题，每个原问题均可以转化为与其对称的对偶问题。对偶问题是指每一个线性规划问题都伴随有另一个线性规划问题。原问题与对偶问题之间是互为对偶的关系。没有绝对的原问题，也没有绝对的对偶问题。

用单纯形法求解线性规划问题时，迭代的每一步在得到原问题一个基本可行解的同时，其检验数行各变量检验数的相反数是其对偶问题的一个基本解；在单纯形表中，原问题的松弛变量对应对偶问题的变量，对偶问题的剩余变量对应原问题的变量；这些互相对应的变量如果在一个问题的解中是基变量，则在另一问题的解中是非基变量。1

分类如果一线性规划问题具有无界解，则其对偶问题具有无可行解；

如果一线性规划问题具有无可行解，则其对偶问题具有无界解或无可行解。1

举例例：设原问题如下，分析其对偶问题的性质。

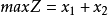
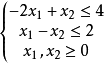
解析：分析可得线性规划原问题是无界的，则其对偶问题具有无可行解。

应用对偶问题在现代数学特别是几何学、代数学、拓扑学等学科中有着广泛的应用，对于推动数学的发展起着很好的作用。举例来讲，在运筹学中运用对偶问题的性质，了解线性规划的无解性内容，明确线性规划问题具有无界解，则其对偶问题具有无可行解；线性规划问题具有无可行解，则其对偶问题具有无界解或无可行解等内容，可以有助于更方便快速的解决实际问题，减少计算时间。2

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所