拉东-尼科迪姆导数又称为测度的相对导数,是点函数的导数概念的推广,拉东-尼科迪姆导数的性质与普通导数的性质十分相似。
简介拉东-尼科迪姆导数又称为测度的相对导数,是点函数的导数概念的推广。
对关于测度v绝对连续的测度μ,存在实值v可测函数f(x),使当A为任意μ可测集时,有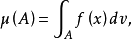 这里的f(x)就称为测度μ相对于v的导数,记为dμ/dv。
这里的f(x)就称为测度μ相对于v的导数,记为dμ/dv。
性质拉东-尼科迪姆导数的性质与普通导数的性质十分相似,例如它的线性运算法则是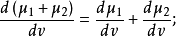 还有链式法则也成立,即若测度μ,v,λ都是σ有限的,且μ⪻v,v⪻λ,则
还有链式法则也成立,即若测度μ,v,λ都是σ有限的,且μ⪻v,v⪻λ,则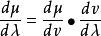 关于测度λ几乎处处成立。
关于测度λ几乎处处成立。
特别地,若μ和v都是Rn的波莱尔子集类上的σ有限测度,f关于v可积,且有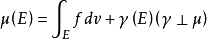 这是由勒贝格定理和拉东-尼科迪姆定理得到的μ的分解,则
这是由勒贝格定理和拉东-尼科迪姆定理得到的μ的分解,则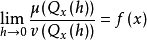 关于测度v对x∈Rn几乎处处成立,其中Qx(h)是以x为中心,边平行于坐标轴且边长为h的n维立方体,即这时测度的相对导数可表为极限,进一步与函数的导数相似。1
关于测度v对x∈Rn几乎处处成立,其中Qx(h)是以x为中心,边平行于坐标轴且边长为h的n维立方体,即这时测度的相对导数可表为极限,进一步与函数的导数相似。1
拉东-尼科迪姆定理拉东-尼科迪姆定理是测度论的重要定理,是牛顿-莱布尼兹公式的推广。
设(Ω,?,μ)是σ有限测度空间,γ是?上的σ有限的广义测度。若γ关于μ绝对连续,则存在Ω上的一个实值μ可测函数f,使得对每个A∈?有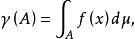 当γ为测度时,可取f为非负可测函数,函数f在关于μ几乎处处相等的意义下是惟一的,f称为广义测度γ关于测度μ的拉东-尼科迪姆导数,记为dγ/dμ。
当γ为测度时,可取f为非负可测函数,函数f在关于μ几乎处处相等的意义下是惟一的,f称为广义测度γ关于测度μ的拉东-尼科迪姆导数,记为dγ/dμ。
本词条内容贡献者为:
李嘉骞 - 博士 - 同济大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国