[科普中国]-伯格曼流形

伯格曼流形是具有伯格曼核函数的一类流形。伯格曼流形的存在性是由于有界域必为伯格曼流形。

简介伯格曼流形是具有伯格曼核函数的一类流形。

伯格曼流形的存在性是由于有界域必为伯格曼流形。

推导设M为n维复流形，Hol(M)为M上所有全纯函数构成的复线性空间，在M上任给测度μ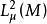，为M上所有适合条件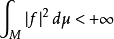的可测函数f构成的复线性空间，记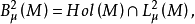在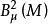中可自然地引进内积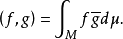如果复流形M适合条件：存在测度μ，使得：

1、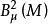关于上述内积为希尔伯特空间。

2、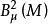有可数基，且在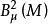中任取规范正交基φ1,φ2,...，使

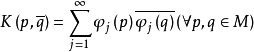为M上关于p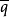，的全纯函数，则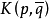有坐标表达式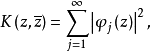做n阶埃尔米特方阵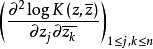于是M上有(1,1)型共变张量场h，它在(U,φ)上有坐标表达式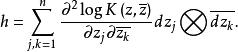在M上有(1,1)型2形式，它在(U,φ)上有坐标表达式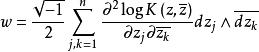且在M上有dw=0。

假设h为M上的埃尔米特度量，则必为克勒度量，这时M称为伯格曼流形，而h称为伯格曼度量。1

本词条内容贡献者为:

李宗秀 - 副教授 - 黑龙江财经学院