[科普中国]-伯利坎普-韦尔奇算法

伯利坎普－韦尔奇算法（英语：Berlekamp-Welch algorithm）是一种用于高效地解码BCH码与里德-所罗门码的算法。

简介伯利坎普－韦尔奇算法（英语：Berlekamp-Welch algorithm）是一种用于高效地解码BCH码与里德-所罗门码的算法，其名取自埃尔温·伯利坎普与劳埃德·韦尔奇。伯利坎普－韦尔奇算法的优点在于这一算法仅需利用矩阵运算。12这一算法的时间复杂度为。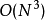

算法伯利坎普－韦尔奇算法通常被用于解码里德-所罗门码。假使在有限体GF(q)上有 n个数字，利用RS码编为n-1次多项式。如果已知传输信道会错误传输 k个值，那么RS码可以传输 P(i)上的n+2k个点(i,P(i))。因此，解码者的问题在于要辨认出哪k个点是错误的。令解码者接收到的点值为R(i)，可以看出对于且仅对于所有正确传输的点i，P(i)=R(i)。

错误辨认多项式伯利坎普－韦尔奇算法引入了错误辨认多项式的概念，也即多项式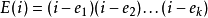，其中e的值为所有k个错误传输的点的i值（均未知）。由于E(i)=0当且仅当i对应一个错误传输的点，可以看出对于所有i值，，其中R(i)对于所有i均为已知常量。令Q(i)=R(i)E(i)，可以看出左侧为一个n+k-1次的多项式，右侧为一个k次的多项式，但其最高次系数为1。因此，整个线性系统有n+2k个方程式与n+2k个未知数，可以用线性代数的方法解出，并可以由P(i)=Q(i)/E(i)解出原始的编码多项式并读出编码值。

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学