商度量空间是度量空间的一种,一个拓扑空间是序列的,当且仅当该空间是个度量空间的商空间。
介绍在数学中,度量空间是个具有距离函数的集合,该距离函数定义集合内所有元素间之距离。此一距离函数被称为集合上的度量。1
度量空间中最符合人们对于现实直观理解的为三维欧几里得空间。事实上,“度量”的概念即是欧几里得距离四个周知的性质之推广。欧几里得度量定义了两点间之距离为连接这两点的直线段之长度。此外,亦存在其他的度量空间,如椭圆几何与双曲几何,而在球体上以角度量测之距离亦为一度量。狭义相对论使用双曲几何的双曲面模型,作为速度之度量空间。
度量空间还能导出开集与闭集之类的拓扑性质,这导致了对更抽象的拓扑空间之研究。
若 M 为度量空间,其度量为 d,且 ~ 为 M 上之等价关系,则可在商集合 M/~ 上赋加下面的(伪)度量。给定两个等价类 [x] 与 [y],可定义
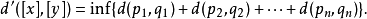
其中,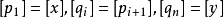 (即取从 [x] 至 [y] 经过所有等价类之路径的最短长度)。一般来说,这仅能定义出一个伪度量,即 d'([x],[y])=0 不一定蕴涵 [x] = [y]。不过,对于良好的等价关系(如将多面体沿着面胶合),则会是个度量。此外,若 M 是个紧致空间,则该度量在 M/~ 上导出之拓扑为商拓扑。
(即取从 [x] 至 [y] 经过所有等价类之路径的最短长度)。一般来说,这仅能定义出一个伪度量,即 d'([x],[y])=0 不一定蕴涵 [x] = [y]。不过,对于良好的等价关系(如将多面体沿着面胶合),则会是个度量。此外,若 M 是个紧致空间,则该度量在 M/~ 上导出之拓扑为商拓扑。
商度量 d 具有下列泛性质:若 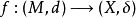 是个度量空间之间的度量映射(即对于所有 x、y,
是个度量空间之间的度量映射(即对于所有 x、y,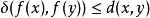 ),满足当
),满足当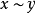 时,f(x)=f(y) 的条件,则函数
时,f(x)=f(y) 的条件,则函数 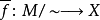 定义为
定义为 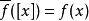 ,亦会是个度量映射
,亦会是个度量映射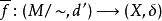 。
。
一个拓扑空间是序列的,当且仅当该空间是个度量空间的商空间。
度量空间的推广每个度量空间都自然会是个一致空间,而每个一致空间也都自然会是个拓扑空间。因此,一致空间与拓扑空间均可视为度量空间的推广。2
若考量上面给定之度量空间的第一个定义,放宽定义中的第二个条件,则可得到伪度量空间。若移除第三个或第四个条件,则可分别得到拟度量空间与半度量空间。
若距离函数的对应域为扩展实数线R∪{+∞},定义中的四个条件维持不变,则称该空间为扩展度量空间。若距离函数的对应域为某个(适当的)有序集(且三角不等式有对应的调整),则可得出“扩展超度量”这个概念。
趋近空间是度量空间的推广,以点对集合的距离取代点对点的距离。
连续性空间是度量空间与偏序集的推广,用来统整度量空间与域的概念。
部分度量空间是为了对度量空间作最小化的推广,使得每个点对自身的距离不再一定为零。
度量空间等价性的概念度量空间之间有着不同的等价性。依据两个空间之间能够存在的函数,可给出不同等价的程度与类型。
给定两个度量空间 (M1,d1) 和 (M2,d2):
这两个空间称之为同胚(拓扑同构)的,若存在两者间的同胚(即两个方向均为连续的双射)。在此条件下,这两个空间能导出相同的拓扑空间。
这两个空间称之为一致同构的,若存在两者间的一致同构(即两个方向均为一致连续的双射)。
这两个空间称之为等距同构的,若存在两者间的等距同构双射。在此一条件下,两个度量空间基本上是相同的。
这两个空间称之为拟等距同构的,若存在两者间的拟等距同构。
参见三角不等式
利普希茨连续
等距同构,压缩映射和度量映射
范数
本词条内容贡献者为:
李宗秀 - 副教授 - 黑龙江财经学院




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国