[科普中国]-瓦尼尔函数

瓦尼尔函数（Wannier function，或沃尼埃函数），是固体物理学中的一个正交函数的完备集，由格里高利·瓦尼尔提出。瓦尼尔函数在晶系中对应着局域化分子轨道。1

晶体中不同晶位的瓦尼尔函数所具有的正交性，使得对特定区域中的电子态进行展开时可以构造出便于计算的基组。瓦尼尔函数的应用极其广泛，例如对电子结合能的分析，在对激子以及里德伯物质的分析中也有其特定的应用。

定义诚然，正如局域化分子轨道，瓦尼尔函数也有许多选取的方式，但最原始的，最简单的，且最常见的定义如下：

选定晶体中的某单一能带，将其布洛赫态标记为

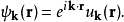其中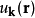 的周期性和晶体的相同。于是瓦尼尔函数就被定义为

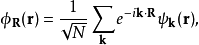
R表示任意格矢（即对于每一布拉维格矢都有一与其对应的瓦尼尔函数）；

N为晶格中原胞的数量；

对k的求和包含布里渊区（或倒易点阵中满足周期性边界条件的原胞）中的N个不同的k，均匀地分布在整个布里渊区内。由于{\displaystyle N}的值通常较大，为了简化运算会使用如下关系来把此求和化为积分：

其中的“BZ”表示布里渊区，其体积为Ω。

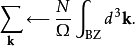
现代的极化理论最近的研究将瓦尼尔函数应用到描述晶体中的极化现象中，例如铁电性。电极化的现代理论解释是由Raffaele Resta和David Vanderbilt提出的，2参见Berghold，和Nakhmanson所发表的文章，以及Vanderbilt的介绍。固体中每一单位晶胞的极化强度可被定义为瓦尼尔电荷密度的电偶极矩：

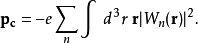
其中的求和符号是对所有占据能带的求和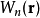，指的是对于能带 n 局域于晶胞中的瓦尼尔函数。在连续的物理过程中，极化强度的变化即为极化的时间导数，可用布洛赫占有态的贝里相位确切地阐述。

参见轨道磁化

布洛赫波

Hannay角

几何相位

本词条内容贡献者为:

尹维龙 - 副教授 - 哈尔滨工业大学