[科普中国]-拉东-尼科迪姆定理

拉东-尼科迪姆定理是测度论的重要定理，是牛顿-莱布尼兹公式的推广。拉东-尼科迪姆导数具有通常点函数导数的某些性质。

简介拉东-尼科迪姆定理是测度论的重要定理，是牛顿-莱布尼兹公式的推广。

设(Ω,?,μ)是σ有限测度空间，γ是?上的σ有限的广义测度。若γ关于μ绝对连续，则存在Ω上的一个实值μ可测函数f，使得对每个A∈?有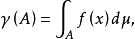 当γ为测度时，可取f为非负可测函数，函数f在关于μ几乎处处相等的意义下是惟一的，f称为广义测度γ关于测度μ的拉东-尼科迪姆导数，记为dγ/dμ。拉东-尼科迪姆导数具有通常点函数导数的某些性质。

发展积分运算从诞生的时候起，就显示了与微分运算的密切联系。

牛顿与莱布尼兹首先从几何上发现了下述微积分基本定理，即牛顿-莱布尼兹公式：设F(x)在[a,b]上可导，且导函数F'(x)=f(x)在[a,b]上黎曼可积，则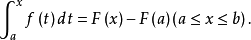

但一般地，F(x)在[a,b]上的导函数F'(x)即使有界，也不一定是黎曼可积的，沃尔泰拉于1881年就构造了这样的例子，这就使在分析数学中至关重要的微积分基本定理的应用收到了限制。

勒贝格于1902年引入了一类新的积分--勒贝格积分，并于1904年证明了，在[a,b]上按他的意义可积的函数f(z)的变上限的积分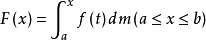 这对[a,b]上几乎所有的点x，导数F'(x)存在且等于f(x)。

维塔利于1905年引入了绝对连续函数的概念，并且证明了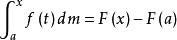 成立的充分必要条件是F'(x)=f(x)a.e.于[a,b]，且F(x)在[a,b]上上绝对连续的。勒贝格积分扩大了使微积分基本定理成立的函数类。

拉东于1913年把它推广到定义在n维欧氏空间中的波莱尔测度的情形。

尼科迪姆(Nikodym,O.M.)于1929年进一步推广到测度空间上的积分。1

测度论测度论是研究一般集合上的测度和积分的理论。它是勒贝格测度和勒贝格积分理论的进一步抽象和发展，又称为抽象测度论或抽象积分论，是现代分析数学中重要工具之一。 测度理论是实变函数论的基础。

测度理论是实变函数论的基础。所谓测度，通俗的讲就是测量几何区域的尺度。 我们知道直线上的闭区间的测度就是通常的线段长度； 平面上一个闭圆盘的测度就是它的面积。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学