[科普中国]-CW复形

CW复形是由一些（有限多个或无穷多个）胞腔从低维到高维逐层堆积而成的空间。

简介CW复形是划分为各维胞腔的豪斯多夫空间。

一个CW复形是由称为基础空间的豪斯多夫空间K和K划分为不相交子集全体{ed}构成的，使下述条件满足：

1、每个ed拓扑地是一个n(d)>0维的开胞腔。进而，对每个胞腔ed，存在一个连续映射f:Dn(d)→K，它把圆盘Dn(d)的内部同胚地映到ed上（f称为胞腔ed的特征映射）；

2、属于闭包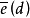 而不属于ed的每个点，必定位于低维胞腔eβ中；

3、闭包有限性。K的每点包含在一个有限的子复形中；

4、怀特海拓扑。K的拓扑为它的有限子复形的顺向极限，即K的一个子集是闭的当且仅当它与每个有限子复形的交是闭的。1

应用单纯复形是CW复形的特例。同伦论中往往需要在拓扑空间上定义满足某种条件的连续映射，这对非常一般的拓扑空间来说很难着手。但对于CW复形，则可以从低维到高维，在一个一个胞腔上给出定义，即采用“逐层扩张”的方式得到所需要的连续映射。

如果扩张到某一层遇到阻碍，就产生阻碍上闭链，阻碍上同调类等，这样就能利用同调来讨论关于连续映射的扩张或同伦等问题。

豪斯多夫空间拓扑学和相关的数学分支中，豪斯多夫空间、分离空间或T2 空间是其中的点都“由邻域分离”的拓扑空间。在众多可施加在拓扑空间上的分离公理中，“豪斯多夫条件”是最常使用和讨论的。它蕴涵了序列、网和滤子的极限的唯一性。豪斯多夫得名于拓扑学的创立者之一费利克斯·豪斯多夫。豪斯多夫最初的拓扑空间定义把豪斯多夫条件包括为公理。

本词条内容贡献者为:

李嘉骞 - 博士 - 同济大学