[科普中国]-普拉托问题

在空间内以给定的闭曲线为边缘张以肥皂膜时，表面张力使膜稳定在表面积为最小的状态。这刺激了科学家对极小曲面的研究。因此，极小曲面问题又称为普拉托问题。

简介1873年，普拉托(Plateau,J.A.F.)曾用实验的方法显示极小曲面。在空间内以给定的闭曲线为边缘张以肥皂膜时，表面张力使膜稳定在表面积为最小的状态。这刺激了科学家对极小曲面的研究。因此，极小曲面问题又称为普拉托问题。

实验过程著名的普拉托实验是把围成封闭曲线的金属丝放入肥皂溶液中，然后取出来，由于表面张力的作用，在它上面就蒙有表面积最小的薄膜。这种表面积最小的曲面就是所谓极小曲面，从数学上求这膜曲面的问题称为普拉托问题。1

求解极小曲面是一种特殊曲面。张在给定的空间闭曲线Γ上有最小面积的曲面称为极小曲面。

在非参数情形下，求极小曲面的问题可以化为求曲面面积泛函

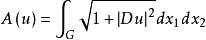的极小值，其中Ω是曲面在x1x2平面上的投影，u是曲面上的点到x1x2平面的距离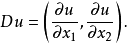，由相应的欧拉-拉格朗日方程可以推出极小曲面的平均曲率处处为零。

由此可见，普拉托问题可以用变分法来解。从变分学观点看，可以考虑以已知闭曲线Γ为固定边界的曲面的法向变分。由欧拉-拉格朗日方程，对于任何这样的变分，曲面面积达到临界值的充要条件是曲面的平均曲率h为0。因此，通常就用这个几何条件来定义极小曲面。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所