[科普中国]-格拉斯曼代数

格拉斯曼代数（Grassmann algebra）是各阶反变张量空间的并构成的代数，又称为外代数。

简介格拉斯曼代数是各阶反变张量空间的并构成的代数。

用Λ(V)记形式和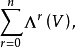则Λ(V)是2维向量空间，设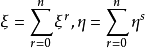，其中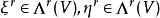。ξ与η的外积是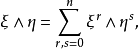则Λ(V)关于外积成为一个代数，成为向量空间的格拉斯曼代数，又称为外代数。向量空间Λ(V)的基底是

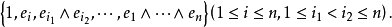
对偶空间对偶空间V*的格拉斯曼代数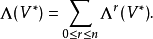Λr(V*)的元素称为向量空间上的r次外形式，它是V上反对称r重线性函数。1

张量空间(tensor space)

张量空间是多重线性代数的重要概念，定义是有张映射的一种向量空间。多重线性代数式代数学的一个重要分支。可以将它看做是线性代数的发展。

张量空间是伴随着微分几何、现代分析、群表示论、理论物理、量子力学等学科发展起来的，并且在这些学科中已得到重要的应用。

本词条内容贡献者为:

杨荣佳 - 教授 - 河北大学