[科普中国]-乘方

定义

求n个相同因数乘积的运算，叫做乘方，乘方的结果叫做幂(power)。其中，a叫做底数(base number)，n叫做指数(exponent)，当aⁿ看作a的n次乘方的结果时，也可读作“a的n次幂”或“a的n次方”。

注：下面的讨论中，底数均不为0。

常用公式同底数幂法则同底数幂相乘除，原来的底数作底数，指数的和或差作指数。1

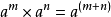
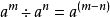
例如：

1） ；

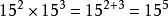2） ；

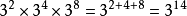3）

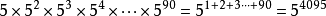
推导示例：

设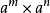 中，m=2，n=4，那么

=

=

=

=

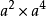
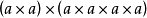
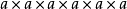
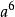
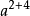
正整数指数幂法则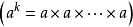 ，其中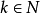 *（即k为正整数）

指数为0幂法则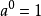 ，其中 ， *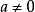

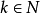推导：

=

=

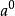
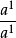
=1

负整数指数幂法则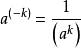 ，其中 ， *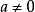

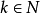推导：

=

=

=

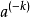
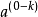
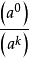
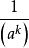
正分数指数幂法则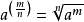 ，其中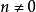 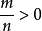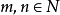， ， *（即m,n为正整数）

负分数指数幂法则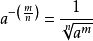 ，其中， ， ， ， *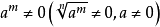

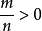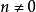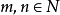推导：

=

=

=

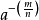
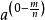
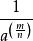
=1/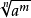

=

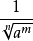
分数指数幂时，当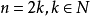 *， 且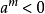 时，则该数在实数范围内无意义

特别地，0的非正数指数幂没有意义2

平方差两数和乘两数差等于它们的平方差。

用字母表示为：

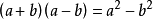
推导：

=

=

=

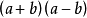
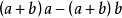
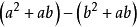
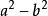
分数的乘方法则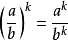

证明：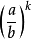

=

=

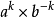
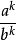
幂的乘方法则幂的乘方，底数不变，指数相乘。

用字母表示为：

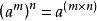
特别指出：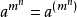

积的乘方积的乘方，先把积中的每一个因数分别乘方，再把所得的幂相乘。

用字母表示为：

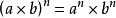
这个积的乘方法则也适用于三个以上乘数积的乘方。如：

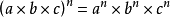
同指数幂乘法同指数幂相乘，指数不变，底数相乘****。

用字母表示为：

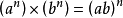
完全平方两数和（或差）的平方，等于它们的平方的和加上（或者减去）它们的积的2倍。

用字母表示为：

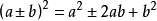
我们一般把它叫作完全平方公式。

立方差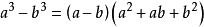

多项式平方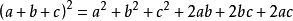

二项式艾萨克·牛顿发现了二项式。二项式是乘方里的复杂运算。右图为二项式计算法则。一般来说，二项式的各项系数按排列顺序也可以这样表示：

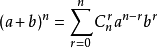
1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…… …… ……

这就是著名的杨辉三角。

有理数乘方的符号法则（1）负数的偶次幂是正数，负数的奇数幂是负数。

( 2)正数的任何次幂都是正数。

（3）0的任何正数次幂都是0。

速算有些较特殊的数的平方，掌握规律后，可以使计算速度加快，现介绍如下。

由n个1组成的数的平方

我们观察下面的例子。

1²=1

11²=121

111²=12321

1111²=1234321

11111²=123454321

111111²=12345654321

……

由以上例子可以看出这样一个规律；求由n个1组成的数的平方，先由1写到n，再由n写到1，即：

11…1**（n个1）**²=1234…(n-1)n(n-1)…4321

注意：其中n只占一个数位，满10应向前进位，当然，这样的速算不宜位数过多。

由n个3组成的数的平方

我们仍观察具体实例：

3²=9

33²=1089

333²=110889

3333²=11108889

33333²=1111088889

由此可知：

33…3**（n个3）² = 11…11[(n-1)个1]** 0 88…88[(n-1)个8] 9

个位是5的数的平方

把a看作10的个数，这样个位数字是5的数的平方可以写成；(10a+5)²的形式。根据完全平方式推导；

=

=

=

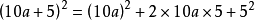
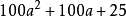
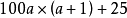
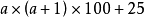
由此可知：**个位数字是5的数的平方，等于去掉个位数字后，所得的数与比这个数大1的数相乘的积，**后面再写上25。

科学记数法一个绝对值大于等于1的数可以写成 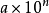（其中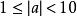，，且n为正整数）的形式叫做科学记数法 例如： 、

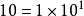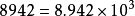
当是负整数指数幂的时候，绝对值小于1的数也可以用科学记数法表示。例如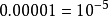： ，即绝对值小于1的数也可以用科学记数法表示为 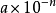的形式，其中 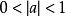， 是正整数。

任何非0实数的0次方都等于1。3

pascal语言实现自然数乘方注意:只能用于求底数、指数均为自然数,且幂不大于2147483647的乘方运算,否则会出错.

var a,b,c,i:longint;{longint的范围较大,为[-2147483648,2147483647]上所有整数}beginc:=1;{因为正整数的0次方均为1}readln(a,b);{输入底数,指数}if (a=0) and (b=0) then writeln('无效输入');{0的0次方无意义}for i:=1 to b do c:=c*a;{for循环实现计算c=a^b}writeln(c);{输出c}end.