定义移位算子
定义1 移位算子(shift operator):将希尔伯特空间中规范正交基的每一个基向量的位置向前(后)移动一位或若干位的线性算子。1
单侧/双侧移位算子定义2 设H是复希尔伯特空间,{en}n=0,1,2,...是H的规范正交基,由
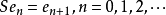 所确定的线性算子S称为重复度为1的单侧移位(或单侧平移)算子。1
所确定的线性算子S称为重复度为1的单侧移位(或单侧平移)算子。1
注:单侧移位算子是次正规算子。1
定义3 设H是复希尔伯特空间,{en}n=0,±1,±2,...是H的一个规范正交基,由
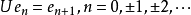 所确定的线性算子称为重复度为1的双侧移位(或双侧平移)算子。1
所确定的线性算子称为重复度为1的双侧移位(或双侧平移)算子。1
定义4 设α是一个基数,α个重复度为1的单(双)侧移位算子的正交和称为重复度为α的单(双)侧移位算子。1
注:单、双侧移位算子统称为移位算子。1
性质1.S和U分别是重复度为α的单、双侧移位算子时,S必是等距算子,U必是酉算子,且U必是S的正规扩张(当α有限时还是最小正规扩张).σ(S)={λ||λ|≤1},σ(U)={λ||λ|=1}.1
2.若S和U是重复度为1的移位算子,则其共轭算子由
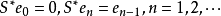 和
和
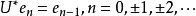 确定。1
确定。1
举例在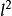 上定义算子U:
上定义算子U:
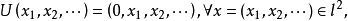 显然,算子U是
显然,算子U是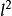 上的右移算子。2
上的右移算子。2
推广-加权移位算子加权移位算子(weighted shift operator)是移位算子的推广,定义如下。
定义51 设H是希尔伯特空间,{en}n=0,1,2,...是H的规范正交基,{wn}n=1,2,...是一个数列,则由
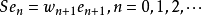 确定的线性算子称为单侧加权移位算子;而{wn}n=1,2,...称为S的权序列。
确定的线性算子称为单侧加权移位算子;而{wn}n=1,2,...称为S的权序列。
设{en}n=0,±1,±2,...是H的规范正交基,类似可定义权序列为{wn}n=0,±1,±2,..的双侧加权移位算子W:
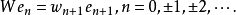
注1:1.单、双侧加权移位算子统称加权移位算子。
2.若S和W是重复度为1的加权移位算子,则S和W的共轭算子由
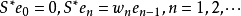 和
和
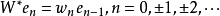 确定。
确定。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国